I was studying from a Linear Algebra textbook when I came across an optional chapter of polynomials. One theorem states that:
Every nonconstant polynomial with complex coefficients has a zero in C.
I’m not exactly sure what best way to describe it in layman’s terms, but it made me think of polynomials in algebra where there are no “real” solutions. A classic example would be:
Think of a (real) number where you multiply by itself then add one becomes 0. The high school algebra answer would be there are no real solutions, but why do they always say “no real solutions” and not “no solutions”? Because as the theorem says, the solution, or the “zero”, is in C.
C is the set of complex numbers in the number system, and a complex number is a number with a real and imaginary component. By definition, every real number is a complex number with the imaginary component being zero.
The “zero” of a polynomial is the value of some variable x such that the polynomial is equal to 0. Another way to look at it is the value of x when the graph of the polynomial crosses the x axis.
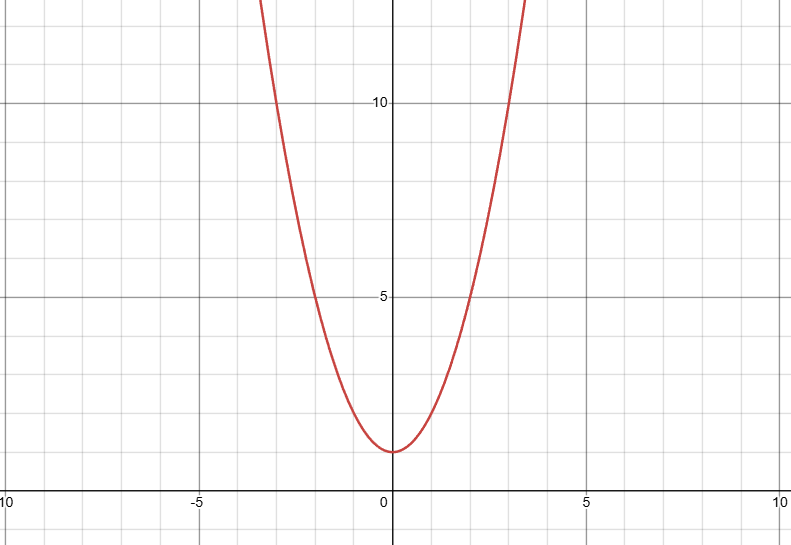
While the image above does not touch the x-axis, if you graph the same polynomial in a complex plane, it will touch the x-axis! (I couldn’t find a nice complex plane graphing calculator to prove my point but just imagine that it does).
What’s interesting in this theorem is the fact that every nonconstant polynomial has a zero, so long as the coefficients are complex numbers.
Tangent to this idea, I wondered if there are noncomplex numbers. You see, when describing the number system it always describes the set of complex numbers as the entirety of all numbers, but are there really numbers outside that space?
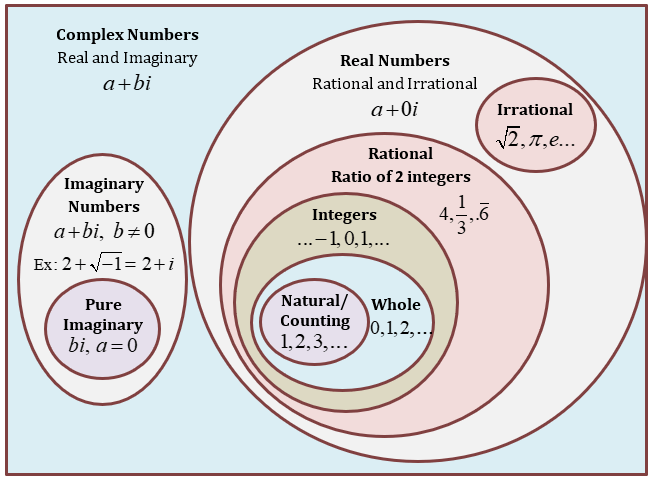
(Image source: mathhints.com)
I’ve seen some forums answer that there are, indeed, noncomplex numbers. I’m not sure if I have the time or energy to explore that answer, but it would be a lovely thing to stumble upon if I did.
Leave a comment